フェネックギツネを折りました。
過去に折った九尾の狐の 構造でなんかできないかなと思ったら小一時間でできたので作ったった感は全然ないのですが、折り出しは必死で考えたので残しておきます。

これが展開図。正三角形が3つ盛り込まれていますがこれを折りだすのが難しい。

この正三角形を折り出せればよいわけです。
対角線と接している点は、対角線を1:(√3+1)/2に内分しています。

4分の1のところで折り筋をつけます。
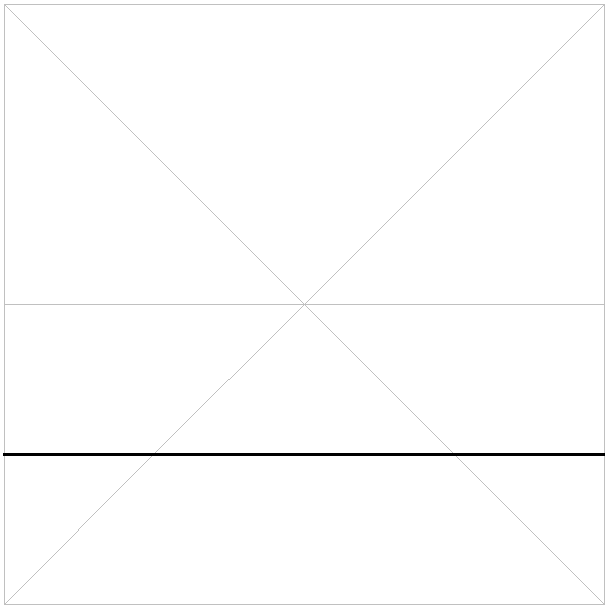
22.5度の線をつけます。
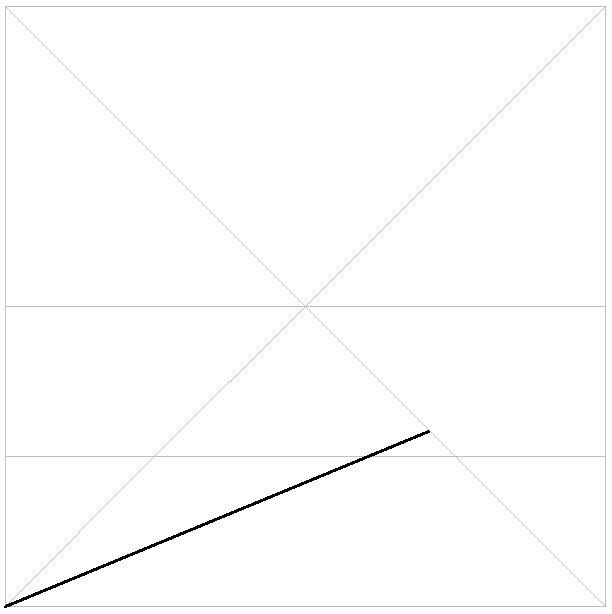
角から4分の1の線と対角線の交点 までの長さと同じ長さのところでフチに印をつけます。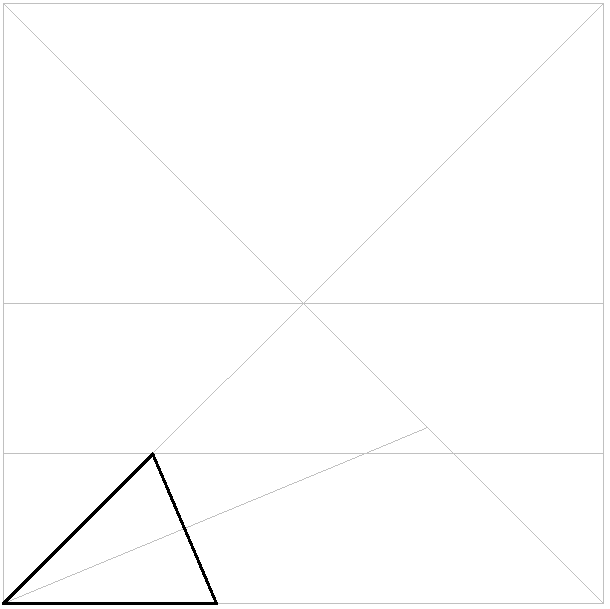
1:√2:√3の三角形ができます。
この三角形に注目します。

3と√3の間の角の二等分線と対辺の交点は、3:√3になりますね。

その点を通りフチに平行な折り筋をつけます。対角線を3:√3に内分する点がわかります。
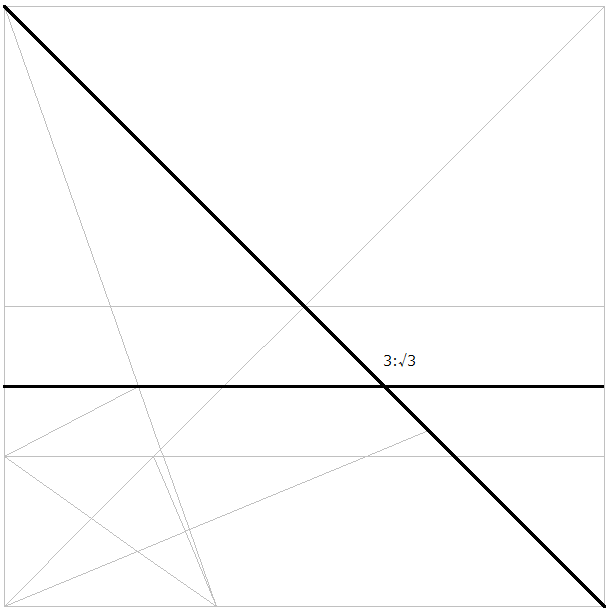
さらに上側の部分を2:1に内分する点を求めていきます。 上側の半分のところで折り筋をつけます。

図のように折り筋をつけます。
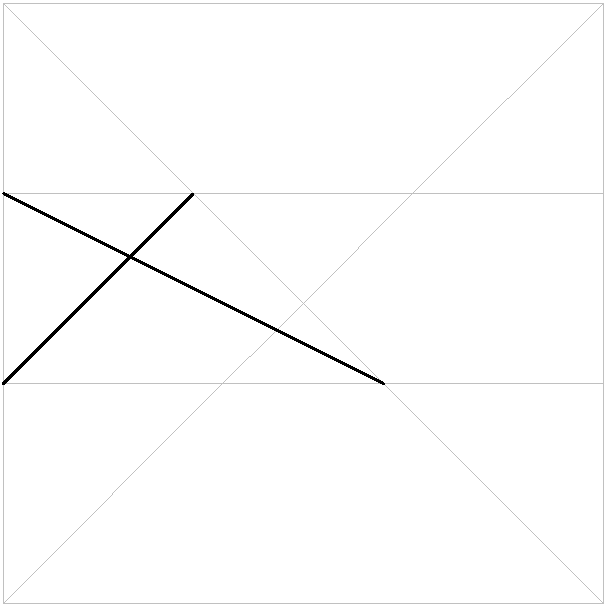
交点を通りフチと平行な折り筋をつけます。ここで対角線が2:1+√3
、すなわち1:(√3+1)/2に内分できました。

対角線に平行な折り筋をつけます。

線分の半分のところで折り筋をつけます。

求まりました。
もっとシンプルなやり方もあるのかもしれませんが、現状手順が多すぎる(=最終的にズレやすい)、余計な折り筋が大量に発生することがデメリットです。しかし結構紙を効率良く使えるという点ではいいかも。
